술취한 승객 문제(C++)

유튜브 알고리즘이 재밌는 알고리즘 영상을 추천해줘서

정리해보고 직접 짜볼겸 정리해봄

The Drunk Passenger Problem. 술취한 승객 문제로 불리는 문제

위 영상을 토대로 작성한 글

1. 문제

---

간단 설명

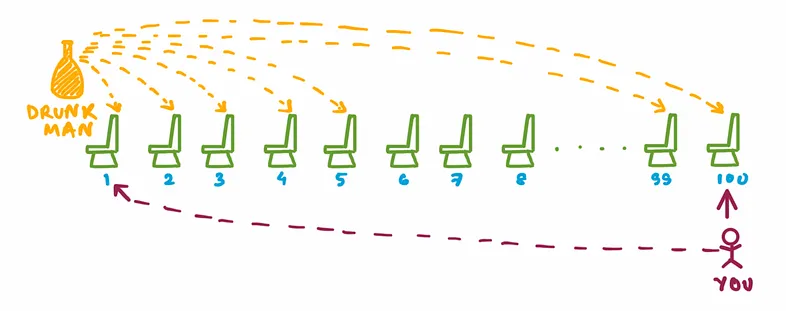
1. 100명의 승객이 있고, 1번부터 100번의 각 승객은 차례로 입장하면서 자신의 좌석표(자기번호)의 자리에 앉는다

2. 그러나 1번 승객이 술에 취해서 아무 자리에나 앉아버렸을 때

3. 100번의 승객이 자기 자리에 앉을 확율을 구하는 문제

• 문제 자체의 이해는 쉬우나 풀이에는 수학적 사고력이 필요한 문제

2. 큰 수의 법칙으로 직접 돌려보자

---

• 가장 간단한 방법은 시뮬레이션 짜서 돌려보고 결과를 확인해보는 큰 수의 법칙(law of large numbers, LLN))

  • 큰수의 법칙 : 경험적 확률과 수학적 확률 사이의 관계를 나타내는 법칙

#include <iostream>
#include <vector>
#include <random>
#include <iterator>

using namespace std;

template<typename Iter, typename RandomGenerator>
Iter select_randomly(Iter start, Iter end, RandomGenerator& g) {
	std::uniform_int_distribution<> dis(0, std::distance(start, end) - 1);
	std::advance(start, dis(g));
	return start;
}

template<typename Iter>
Iter select_randomly(Iter start, Iter end) {
	static std::random_device rd;
	static std::mt19937 gen(rd());
	return select_randomly(start, end, gen);
}

bool trial() {
	bool occupied[101]; // 1~100번 좌석에 사람이 있는지 확인하기 위한 변수
	vector<int> seat_remainder; // 남은 자리
	for (int i = 1; i <= 100; i++) {
		seat_remainder.push_back(i);
		occupied[i] = false;
	}

    // 1번부터 99번까지 앉는다
	for (int i = 1; i < 100; i++) {
		// 술취한 사람이거나, 자기자리를 뺏긴 사람인 경우
		if (i == 1 || occupied[i] == true) {
			int r = *select_randomly(seat_remainder.begin(), seat_remainder.end()); // 남은 자리중에서 랜덤으로 한자리 고르기
			occupied[r] = true; // 앉았음

			seat_remainder.erase(
				remove(seat_remainder.begin(), seat_remainder.end(), r), seat_remainder.end()
			); // 남은 자리 제거 
		} // 자기 자리가 있으면
		else {
			occupied[i] = true; // 자기 자리에 앉는다
			seat_remainder.erase(
				remove(seat_remainder.begin(), seat_remainder.end(), i), seat_remainder.end()
			);
		}
	}

    // 100번 좌석표를 가진 승객이 100번 자리에 앉았는지 못앉았는지는 
    // 100번 승객이 자신의 자리가 비어있는지 여부로 결정된다
	return occupied[100];
}

int main() {
	for (int tc = 1; tc <= 10; tc++) {
		int nums[2] = { 0, 0 };
		for (int i = 0; i < 10000; i++) {
			nums[trial()] += 1; // 성공, 실패 회수 1씩 증가
		}
		printf("TC%d : [%d, %d]\n", tc, nums[0], nums[1]);
	}
	

	return 0;
}

• 파이썬 -> C++ 로 변환하면서 배운것

• C++ 벡터 랜덤 원소 뽑는 random_shuffle은 C++17에서 없어짐. 대신 random 라이브러리 이용해서 구현

• nums[trial()] += 1; 처럼 배열의 원소에 함수 리턴값이 들어갈 수 있다

• 벡터에서 특정 원소 지우는건 할때마다 햇갈림

10번 정도 돌려도 1/2정도 나온다

거의 반반

3. 왜 1/2인가?

---

• 100번 좌석표를 가진 승객이 자리에 못앉는 경우는?

  • 이전 승객이 100번 자리에 이미 앉은 경우!

• 그렇다면 어떤 조건이 발생하면 100번은 무조건 자리에 앉을 수 있는가?

  • 자리를 뺏긴 누군가가 1번 좌석에 앉는 경우

  • 좌석 번호가 얽힌 사람들끼리 문제가 해결됨!

  • 나머지 사람들은 자기 자리를 찾아 앉게 되므로 100번도 자기 자리에 앉을 수 있음

• 모든 랜덤 선택의 순간에서 1을 고를 확률과 100을 고를 확률은 같다

  • ex) 14번이 랜덤 선택을 한다면 1, 15~99, 100 중에 하나 1/87

  • ex) 98번이 랜덤 선택을 한다면 1, 99, 100 중에 하나 1/3

• 모든 순간 100번의 운명은 같은 확률로 갈라짐

  • 1또는 100을 고르지 않는 선택은 선택을 뒤로 미룰뿐이다

그러므로 100번 좌석에 앉을 확률은 1/2이라고 함

더 자세한 수학적 증명은 아래 참조 링크

---

예전에 공학수업 수업시간에

몬티홀 문제를 교수님이 증명해주시는걸 들으면서 꽤나 충격을 받았던적이 있었는데

그런 느낌을 받았다

이런 수학적 증명은 어떻게 하는걸까 대단하다

출처 :

임커밋

The Drunk Passenger Problem