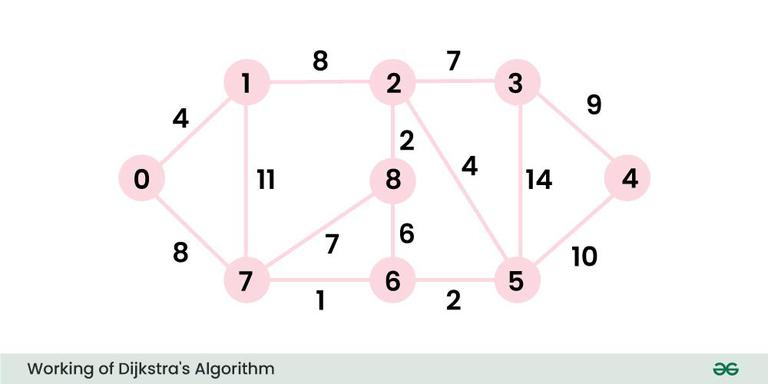
백준 1504. 특정한 최단 경로

특정한 최단 경로

다익스트라 문제 최단경로의 업그레이드 버전

1. 간단 설명

---

꼭 방문해야하는 두 정점이 추가된 문제

주어진 두 정점을 거치면서 최단 경로로 이동하는 프로그램을 작성하기

2. 예시

---

4 6
1 2 3
2 3 3
3 4 1
1 3 5
2 4 5
1 4 4
2 3

다음과 같이 간선 정보가 주어졌을 때,

1에서 4로 도달하는데, 2와 3은 꼭 지나야한다

그렇다면 경로는 (1,2,3,4) 혹은 (1,3,2,4)가 된다

(1,2,3,4) = 3 + 3 + 1 = 7

(1,3,2,4) = 5 + 3 + 5 = 13

(1,2,3,4)를 경로로 할 때, 최단 경로가 7이다

주의사항

경로가 없을땐 -1을 출력해야한다

또한, 값들이 크므로, 오버플로우에 주의해야한다

3. 알고리즘

---

노드가 800개, 간선이 20만개 정도 주어진다

DFS, BFS는 시간초과가 날 것으로 보이므로

최단경로를 구하는 알고리즘은 다익스트라 알고리즘이 적절해보인다

가능한 경로는 총 주가지로

v1을 먼저 들르는 1번 경로 : (1, v1) -> (v1, v2) -> (v2, N)와

v2를 먼저 들르는 2번 경로 : (1, v2) -> (v2, v1) -> (v1, N)로 구분할 수 있다

이 두 경로를 비교한 뒤 최소값을 출력한다

1. N, E 입력받기
2. 맵 정보 입력받기
3. 경로 1 계산
	3-1. (1,v1) 
	3-2. (v1,v2)
	3-3. (v2,N)
4. 경로 2 계산
	4-1. (1,v2)
	4-2. (v2,v1)
	4-3. (v1,N)
5. 경로값 비교 후 최단거리 출력

첫 풀이시에는 다익스트라를 6번 돌렸는데 시간초과가 발생했다

경로 1을 계산할 때 dijkstra(1, v1) + dijkstra(v1,v2) + dijkstra(v2,N)를 각각 구하는 방식을 사용했는데

실제로는 두번만 돌리면 된다

1번 경로 : (1,v1), (v1,v2) ,(v2, N)에서 (1, v1)과 (v1, 1)은 양방향 그래프이므로 값이 같다

2번 경로 : (1,v2), (v2,v1), (v1, N)에서도 마찬가지로 (1,v2)과 (v2, 1)은 같다

즉 v1에 대해서 다익스트라를 돌리면 (v1,1), (v1,v2), 경로 2에서 사용하는 (v1, N)을 구할 수 있고

v2에 대해서 다익스트라를 돌리면 (v2, 1), (v2, v1), 경로 1에서 사용하는 (v2,N)을 구할 수 있다

이 구한값을을 더해서 최소값을 출력하면된다

필요 변수

• 노드와 간선의 개수 int N, E (2 ≤ N ≤ 800, 0 ≤ E ≤ 200,000)
• 간선 정보를 저장할 맵 vector< pair<int, int> > map[MAX]
• 경유지 int v1, v2
• 다익스트라
  • 경로 값을 저장할 int d[MAX]
  • 우선순위 큐를 이용한 다익스트라 사용 prioirty_queue<pair<int, int >> pq

4. 소스코드

---

#include <iostream>
#include <vector>
#include <queue>

#define MAX 801

using namespace std;

int N, E;
vector< pair<int, int> > map[MAX];
int v1, v2;
long long int d[MAX]; 

void Input() {
	freopen_s(new FILE*, "input.txt", "r", stdin);
	cin >> N >> E;
	for (int i = 0; i < E; i++) {
		int start, end, val;
		cin >> start >> end >> val;
		map[start].push_back({ end,val });
		map[end].push_back({ start,val });
	}
	cin >> v1 >> v2;
}

void Dijkstra(int start) {
	for (int i = 1; i <= N; i++) {
		d[i] = 21e8;
	}

	d[start] = 0; 

	priority_queue < pair<int, int> > pq; // 노드, 거리

	pq.push({ start, 0 });

	while (!pq.empty()) {
		int cur = pq.top().first;
		int dis = pq.top().second * -1;
		pq.pop();

		if (d[cur] < dis) continue;

		for (int i = 0; i < map[cur].size(); i++) {
			int next = map[cur][i].first;
			int nextDis = dis + map[cur][i].second;

			if (nextDis < d[next]) {
				d[next] = nextDis;
				pq.push({ next, nextDis * -1 });
			}
		}
	}
}

int main() {

	Input();

	long long int v1_1, v1_v2, v1_n, v2_1, v2_v1, v2_n;
	Dijkstra(v1);
	v1_1 = d[1];
	v1_v2 = d[v2];
	v1_n = d[N];
	Dijkstra(v2);
	v2_1 = d[1];
	v2_v1 = d[v1];
	v2_n = d[N];
	
	long long int res1 = v1_1 + v1_v2 + v2_n;
	long long int res2 = v2_1 + v2_v1 + v1_n;

	if (res1 >= 21e8 && res2 >= 21e8) {
		cout << -1;
		return 0;
	}

	if (res1 < res2)
		cout << res1;
	else 
		cout << res2;
	
	return 0;
}

다익스트라를 직접 구현하려니 생각처럼 쉽지 않았다

연습을 더 많이 해야겠다